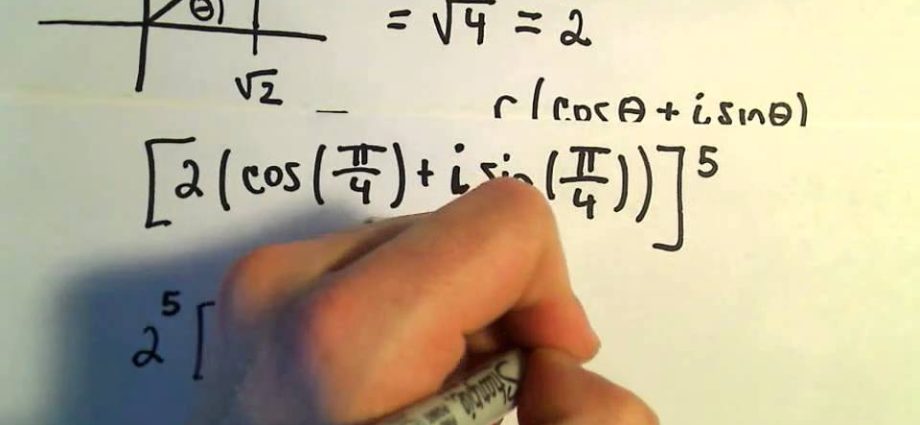복소수를 자연제곱으로 올리기

이 간행물에서 우리는 복소수를 거듭제곱하는 방법을 고려할 것입니다(De Moivre 공식 사용 포함). 이론적인 자료는 더 나은 이해를 위해 예제와 함께 제공됩니다.

복소수를 거듭제곱하기

먼저 복소수는 다음과 같은 일반 형식을 갖는다는 것을 기억하십시오. z = a + 바이 (대수적 형태).

이제 문제 해결을 직접 진행할 수 있습니다.

제곱수

정도를 같은 요인의 곱으로 나타낼 수 있고 그 곱을 찾을 수 있습니다(기억하면서 i² = -1).

z² = (아 + 바이)² = (a + 바이)(a + 바이)

예 1 :

z=3+5i

z² = (3 + 5i)² = (3 + 5i)(3 + 5i) = 9 + 15i + 15i + 25i² = -16 + 30i

다음과 같이 합계의 제곱을 사용할 수도 있습니다.

z² = (아 + 바이)² = a² + 2 ⋅ a ⋅ 바이 + (바이)² = a² + 2abi – b²

참고 : 마찬가지로 필요한 경우 차이의 제곱, 합/차의 세제곱 등에 대한 공식을 얻을 수 있습니다.

N번째 학위

복소수 올리기 z 종류 n 삼각법 형식으로 표현하면 훨씬 쉽습니다.

일반적으로 숫자 표기법은 다음과 같습니다. 지 = |지| ⋅ (코사인 φ + i ⋅ 죄 φ).

지수의 경우 다음을 사용할 수 있습니다. 드 무아브르의 공식 (영국 수학자 Abraham de Moivre의 이름을 따서 명명됨):

zⁿ = | 지 |ⁿ ⋅ (코사인(nφ) + i ⋅ 죄(nφ))

수식은 삼각법 형식으로 작성하여 얻습니다(모듈이 곱해지고 인수가 추가됨).

예제 2

복소수 올리기 z = 2 ⋅ (cos 35° + i ⋅ sin 35°) 여덟 번째 정도.

해법

z⁸ = 2⁸ ⋅ (cos(8 ⋅ 35°) + i ⋅ sin(8 ⋅ 35°)) = 256 ⋅ (cos 280° + i sin 280°).